Perspektivní projekce

Jak jsem již zmínil, krychle je třírozměrná, ale obrazovka je jen dvourozměrná. Pokud tedy chceme krychli nakreslit na obrazovku musíme její jednotlivé vrcholy nějak zobrazit do roviny. Jedna možnost by byla ortogonální projekce. Nicméně výsledek by nebyl přirozený, protože lidské oko nevnímá svět pomocí ortogonální projekce. Realističtější možnost je použít perspektivní projekci. Každý ji jistě zná z vlastní zkušenosti, např. víme, že vzdálenější objekty se jeví menší, koleje se v dálce sbíhají do jednoho bodu atd. Více informací lze nalézt třeba zde.

Když se díváme na nějaký objekt, naše oko vnímá světlo odražené od tohoto objektu a mozek nám v hlavě vyrobí jeho obraz. Zjednodušeně můžeme říci, že z každého bodu objektu, který vidíme, letí paprsek světla do našeho oka. Představte si, že naše krychle je kdesi za monitorem a my se na ní díváme skrze monitor. Z každého bodu krychle letí tedy do našeho oka paprsek, který se někde protíná s obrazovkou monitoru. Za monitorem ale žádná krychle není a my chceme na obrazovku nakreslit jako by tam byla. Zvolíme nějaký pevný bod před obrazovkou, kde budeme předpokládat, že je oko pozorovatele. Pak vezmeme naší hypotetickou krychli za monitorem a z každého vrcholu (který vidíme) hypotetické krychle vyšleme paprsek do tohoto pevného bodu. Následně spočítáme, kde se ony paprsky protnou s obrazovkou. Tyto průniky potom udávají, kam nakreslit jednotlivé vrcholy na obrazovku. Pak již stačí spojit body odpovídající jednotlivým stěnám a vzniklé čtyřúhelníky vybarvit barvou krychle.

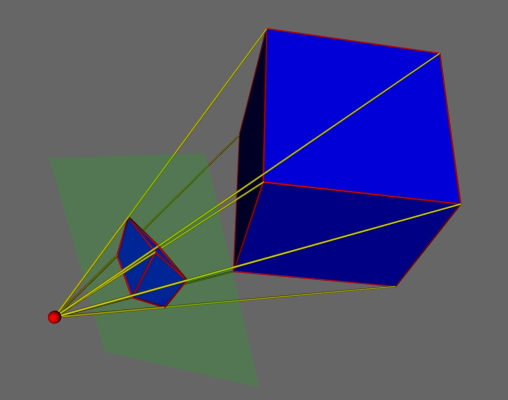
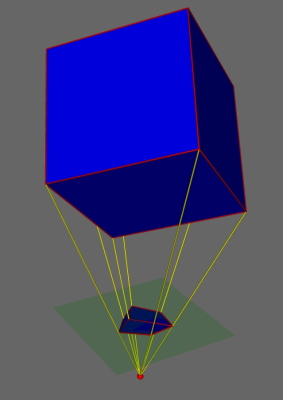
Lépe je to vidět na následujících obrázcích. Červený bod představuje oko pozorovatele, zelená poloprůhledná plocha obrazovku a žluté přímky paprsky směřující z vrcholů do oka.

Pokud si chcete vidět tuto situaci i z jiných směrů, stačí použít tento skript pro program Octave (pozor je nutno mít nainstalované rozšíření Octaviz).

Nyní si tedy můžeme vysvětlit, jak budeme promítat jednotlivé body v 3D prostoru do 2D prostoru. Řekněme, že oko pozorovatele umístíme do bodu $(0,0,0)$. Obrazovku monitoru umístíme do roviny dané rovnicí $z=1$, tj. roviny sestávající se z bodů $(x,y,1)$ pro všechny $x,y\in\mathbb{R}$. Protože naše krychle zadaná maticí points má bod $(0,0,0)$ ve svém středu, musíme krychli posunout tak, aby byla za obrazovkou. Tento posun je zadán vektorem shift $=(0,0,10)$. Vezměme libovolný vrchol naší krychle $\mathbf{v}=(v_1,v_2,v_3)$, který chceme promítnout na obrazovku. Posuneme ho pomocí vektoru shift, tj. dostaneme vektor shift + $\mathbf{v}=(v_1,v_2,v_3+10)$. Paprsek směřující z tohoto vrcholu do oka pozorovatele si můžeme představit jako přímku, která prochází bodem $(0,0,0)$ a má směrový vektor $(v_1,v_2,v_3+10)$. Pokud chceme najít bod, kde se tato přímka protíná s obrazovkou, stačí tento vektor vynásobit vhodným skalárem tak, aby výsledný vektor byl tvaru $(x,y,1)$. Takový skalár je zřejmě $1/(v_3+10)$. Bod průniku tedy je $(v_1/(v_3+10),v_2/(v_3+10),1)$. Souřadnice na obrazovce tedy jsou $(v_1/(v_3+10),v_2/(v_3+10))$. Nakonec musíme z těchto souřadnic vyrobit nějaká smysluplná čísla v pixelech. Nejprve souřadnice vynásobíme vhodným měřítkem scale, aby byla naše krychle dostatečně velká v poměru k velikosti našeho <canvas> tagu. Následně souřadnice posuneme tak, aby bod $(0,0)$ byl ve středu našeho <canvas> tagu. Výše uvedený postup je zachycen ve funkci perpective_projection:

    function perspective_projection(v) {
      var output = [0,0];

      v = v.add(shift);   // posun od pozorovatele.
      output[0] = scale * (v.e(1)/v.e(3)) + x_center;     // vypocet perspektivni projekce
      output[1] = scale * (-v.e(2)/v.e(3)) + y_center;
      
      return(output);
    };