Next: Perspektivní projekce Up: Točíme krychlí Previous: Datové struktury
Jak již bylo zmíněno, po nahrání stránky do prohlížeče se zavolá funkce init():
function init() {
rot = get_rotation_matrix(r,angle); // Spocita matici rotace pro zadany smer osy a uhel o kolik se ma otacet.
setInterval(animate,100); // Nastavi, aby se funkce animate volala kazdy 100ms.
};
Ta nejprve zavolá funkci get_rotation_matrix(r,angle), která spočítá matici rotace rot, a pak
nastaví, aby se funkce animate() volala každých 100ms.
K výpočtu matici rotace rot využijeme faktu, že umíme rotovat s vektory v ![]() okolo počátku o zadaný úhel
okolo počátku o zadaný úhel ![]() .
Nechť
.
Nechť ![]() je libovolná uspořádaná ortonormální báze v
je libovolná uspořádaná ortonormální báze v ![]() . Matici lineárního zobrazení takového otočení vzhledem k bázi
. Matici lineárního zobrazení takového otočení vzhledem k bázi ![]() jsme viděli na přednášce:
jsme viděli na přednášce:
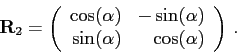
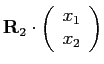 . Výsledkem je matice typu
. Výsledkem je matice typu 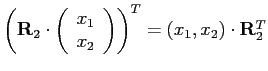 .
.
Nechť nyní
![]() je libovolná uspořádaná ortonormální báze
je libovolná uspořádaná ortonormální báze ![]() .
Matici
.
Matici ![]() otáčení v rovině můžeme snadno rozšířit i do 3D prostoru tak, aby otáčela vektory kolem osy dané
vektorem
otáčení v rovině můžeme snadno rozšířit i do 3D prostoru tak, aby otáčela vektory kolem osy dané
vektorem ![]() . Při takové rotaci totiž zůstává třetí souřadnice konstantní a první dvě se otočí jako v rovině.
Matice rotace vzhledem ke bázi
. Při takové rotaci totiž zůstává třetí souřadnice konstantní a první dvě se otočí jako v rovině.
Matice rotace vzhledem ke bázi ![]() kolem osy dané
kolem osy dané ![]() je tedy takováto matice:
je tedy takováto matice:
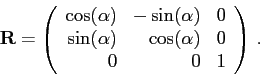
Nechť
![]() je libovolný vektor v
je libovolný vektor v ![]() se souřadnicemi
se souřadnicemi ![]() vzhledem k
vzhledem k ![]() .
Podobně jako předtím v rovině, pokud chceme najít souřadnice otočeného vektoru
.
Podobně jako předtím v rovině, pokud chceme najít souřadnice otočeného vektoru ![]() vzhledem k bázi
vzhledem k bázi ![]() , stačí
spočítat výraz
, stačí
spočítat výraz
![]() .
.
Matice ![]() umí tedy otáčet vektory kolem osy dané vektorem
umí tedy otáčet vektory kolem osy dané vektorem ![]() . Nicméně na to abychom ji mohli použít
na otočení vektoru
. Nicméně na to abychom ji mohli použít
na otočení vektoru
![]() , musíme znát jeho souřadnice v bázi
, musíme znát jeho souřadnice v bázi ![]() . Vektor
. Vektor ![]() máme typicky zadán pomocí
souřadnic vhledem ke standardní bázi
máme typicky zadán pomocí
souřadnic vhledem ke standardní bázi
![]() . Jeho souřadnice vzhledem k bázi
. Jeho souřadnice vzhledem k bázi ![]() získáme pomocí
matice přechodu od
získáme pomocí
matice přechodu od ![]() k
k ![]() . Označme
. Označme
![]() ,
,
![]() a
a
![]() ,
tj.
,
tj. ![]() jsou souřadnice vzhledem k
jsou souřadnice vzhledem k ![]() . Pak snadno získáme matici přechodu
. Pak snadno získáme matici přechodu ![]() od
od ![]() k
k ![]() . Je to totiž
matice identického zobrazení vzhledem k bázím
. Je to totiž
matice identického zobrazení vzhledem k bázím ![]() a
a ![]() , tzn. její sloupce jsou tvořeny souřadnicemi vektorů
, tzn. její sloupce jsou tvořeny souřadnicemi vektorů
![]() vzhledem k
vzhledem k ![]() , tj.
, tj.
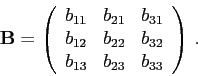
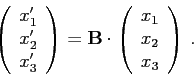
Pokud chceme naopak přepočítat souřadnice
z ![]() do
do ![]() , stačí vynásobit předchozí rovnost
, stačí vynásobit předchozí rovnost
![]() zleva (což je matice přechodu od
zleva (což je matice přechodu od ![]() k
k ![]() ), tj. pokud
vím, že
), tj. pokud
vím, že
![]() , pak
, pak
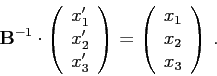
Nyní chceme umět otočit libovolný vektor
![]() podle osy dané
podle osy dané ![]() . Složky uspořádané trojice
. Složky uspořádané trojice
![]() odpovídají souřadnicím vektoru
odpovídají souřadnicím vektoru ![]() vzhledem k bázi
vzhledem k bázi ![]() . Otočený vektor
. Otočený vektor
![]() získáme takto:
získáme takto:
Teď jsme připraveni si vysvětlit, co funkce get_rotation_matrix(r,angle) vlastně dělá. Funkce používá následující proměnné:
var coor_matrix = Matrix.create([
[0,0,0],[0,0,0],[0,0,0]
]);
var rot_matrix = Matrix.create([
[0,0,0],[0,0,0],[0,0,0]
]);
var a = Vector.create([0,0,0]);
var b = Vector.create([0,0,0]);
Proměnná coor_matrix je proměnná pro matici přechodu
Na začátku funkce testuje, jestli není vektor osy rotace r nulový. V případě, že ano, nastaví r na ![]() .
.
if (r.eql(Vector.Zero(3))) {
r.setElements([1,1,1]);
alert("Vektor osy rotace nemuze byt nulovy!");
}
Nyní je potřeba zkonstruovat libovolnou uspořádanou ortonormální bázi, jejíž třetí vektor je r (libovolnou až na pořadí
prvních dvou bázových vektorů, jímž můžeme ovlivnit směr výsledné rotace). Takže potřebujeme najít dva navzájem kolmé vektory
a,b délky ![]() , které budou kolmé na vektor r. Nejprve uděláme z r vektor délky
, které budou kolmé na vektor r. Nejprve uděláme z r vektor délky ![]() . Pak zvolíme libovolný
vektor a délky
. Pak zvolíme libovolný
vektor a délky ![]() , který je na r kolmý. Nechť r
, který je na r kolmý. Nechť r
![]() . Pokud
. Pokud ![]() , pak takový vektor
je např.
, pak takový vektor
je např. ![]() . Pokud alespoň jedno z
. Pokud alespoň jedno z ![]() je nenulové, můžeme vzít např. vektor
je nenulové, můžeme vzít např. vektor ![]() a udělat z něj
vektor délky
a udělat z něj
vektor délky ![]() . Nakonec najdeme vektor b délky
. Nakonec najdeme vektor b délky ![]() , který je kolmý na a i r pomocí vektorového součinu r
, který je kolmý na a i r pomocí vektorového součinu r![]() a.
Výše uvedený postup je obsahem následujícího kusu kódu:
a.
Výše uvedený postup je obsahem následujícího kusu kódu:
r = r.toUnitVector();
if (r.e(1)!=0 || r.e(2)!=0) {
a.setElements([-r.e(2),r.e(1),0]);
a = a.toUnitVector();
}
else {
a.setElements([1,0,0]);
}
b = r.cross(a);
Uspořádaná trojice ![]() =(a,b,r) tvoří uspořádanou ortonormální bázi, jejíž třetí vektor je směrový vektor osy rotace.
Sestavíme matici přechodu od
=(a,b,r) tvoří uspořádanou ortonormální bázi, jejíž třetí vektor je směrový vektor osy rotace.
Sestavíme matici přechodu od ![]() k
k ![]() .
.
coor_matrix.setElements([
[a.e(1),b.e(1),r.e(1)],
[a.e(2),b.e(2),r.e(2)],
[a.e(3),b.e(3),r.e(3)]
]);
Do proměnné rot_matrix zadáme matici ![]() s úhlem
s úhlem ![]() angle:
angle:
rot_matrix.setElements([
[ Math.cos(angle), Math.sin(angle),0],
[-Math.sin(angle), Math.cos(angle),0],
[ 0, 0,1]
]);
Nakonec spočítáme součin
![]() (viz rovnice (2))
a jeho výsledek vrátíme jako výstup funkce:
(viz rovnice (2))
a jeho výsledek vrátíme jako výstup funkce:
rot_matrix = rot_matrix.multiply(coor_matrix.transpose()); // rot_matrix*(coor_matrix)^T
rot_matrix = coor_matrix.multiply(rot_matrix); // coor_matrix*(rot_matrix*(coor_matrix)^T)
return(rot_matrix);
Rostislav Horcik 2009-01-04